Articulated Systems¶

ANYmal robots (B and C versions) simulated in RaiSim.

TL;DR¶

Click the image for vector graphics

Introduction¶

An articulated Systems is a system of multiple bodies connected through joints. There are two types of articulated systems: Kinematic trees and closed-loop systems. Kinematic trees do not contain a loop (a body always has only one parent joint). Consequently, the number of joints is equal to the number of bodies (for floating systems, we assign a floating joint on the root body). RaiSim can only simulate kinematic trees.

Since all bodies have one joint, a body index is always the same as its parent joint’s index. A body refers to a rigid body which is composed of one or more links. All links within a body are connected to each other by a fixed joint.

Creating an instance¶

Just like any other object, an articulated system is created by the world instance using addArticulatedSystem method. There are three ways to specify the system.

by providing the path to the URDF file (the most recommneded way)
by providing std::string of the URDF text (can be useful when working with Xacro)
by providing a raisim::Child instance. It is an advanced method and not recommended for beginners.

Note that option 1 and 2 use the same method. You can provide either the path string or the contents string and the class will identify which one is provided.

To use option 3, you have to provide all details of the robot in C++ code. Child is a tree node which contains fixedBodies and child. It also contains joint, body, and name. All properties should be filled.

State Representation¶

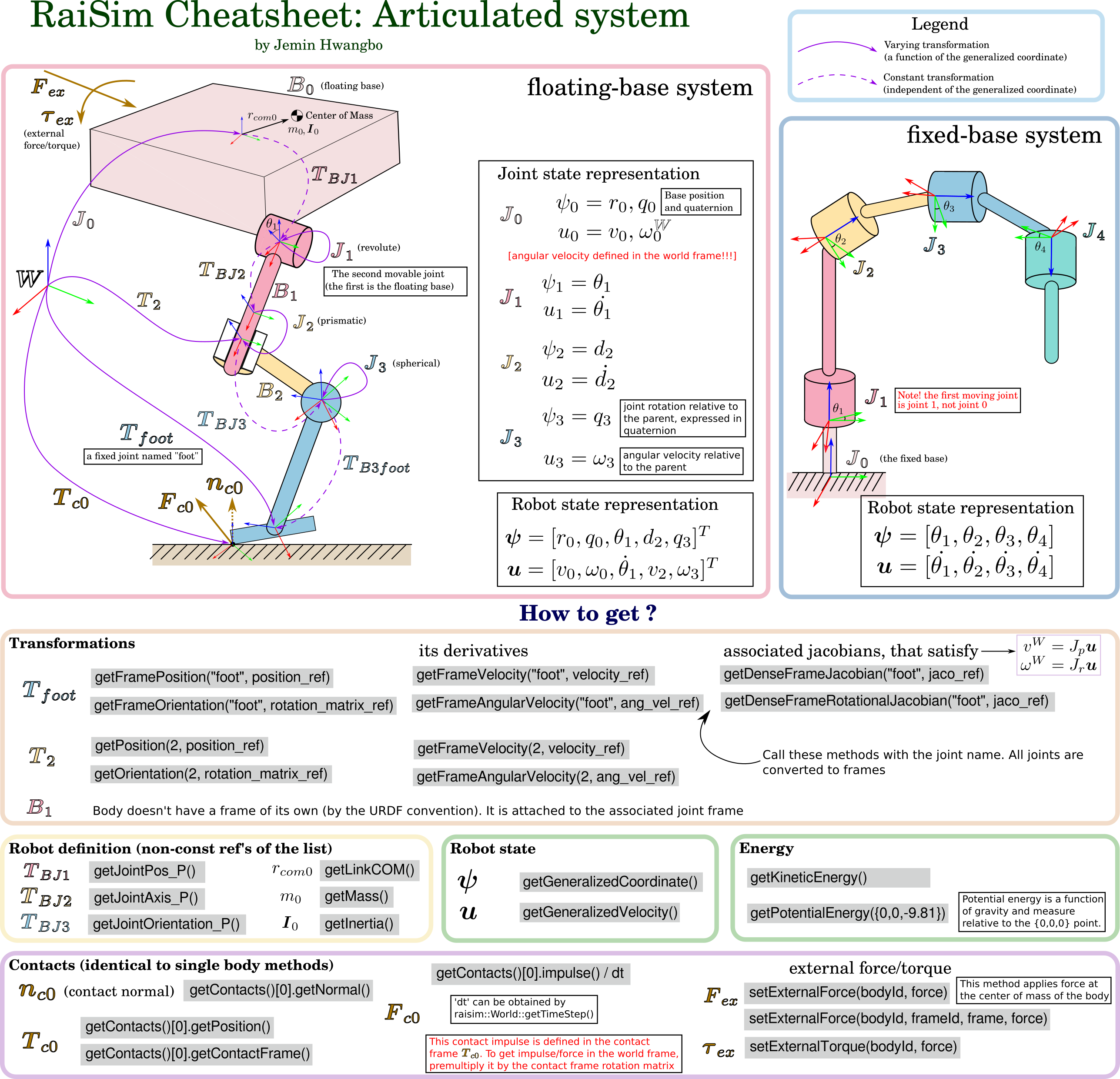
The state of an articulated system can be represented by a generalized state \(\boldsymbol{S}\), which is composed of a generalized coordinate \(\boldsymbol{q}\) and a generalized velocity \(\boldsymbol{u}\). Since we are not constraining their parameterization, in general,

\[\begin{equation} \boldsymbol{u}\neq\dot{\boldsymbol{q}}. \end{equation}\]

A generalized coordinate fully represents the configuration of the articulated system and a generalized velocity fully represents the velocity state of the articulated system.

Every joint has a corresponding generalized coordinate and generalized velocity. A concatenation of all joint generalized coordinates and velocities are the generalized coordinates and velocities of the articulated system, respectively. The order of this concatenation is called joint order. The URDF reader lists joints in the depth first manner. For the joints from the same parent, the joint order is determined by the order the joint appears in the URDF. The joint order can be accessed through getMovableJointNames(). Note the keyword “movable”. The fixed joints contribute to neither the generalized coordinate nor the generalized velocity. Only movable joints do.

The joint order starts with the root body which is the first body of the articulated system. For floating-base systems, the root body is the floating base. For fixed-base systems, the root body is the one rigidly attached to the world. Even though the fixed base cannot move physically, users can move them using setBaseOrientation and setBasePosition. So getMovableJointNames() method will return the fixed base name and the fixed base joint is a part of the joint order.

The following example illustrates how the generalized coordinates and velocities are defined.

To set the state of the system, the following methods can be used

setGeneralizedCoordinate
setGeneralizedVelocity
setState

To obtain the state of the system, the following methods can be used

getGeneralizedCoordinate
getGeneralizedVelocity
getState

The dimensions of each vector can be obtained respectively by

getGeneralizedCoordinateDim
getDOF or getGeneralizedVelocityDim.

These two methods are identical

Joints¶

Here are the available joints in RaiSim.

Joint Properties (\(|\cdot|\) is a symbol for dimension size (i.e., cardinality))¶
	Fixed	Floating	Revolute	Prismatic	Spherical
\(\|\boldsymbol{u}\|\)	0	6	1	1	3
\(\|\boldsymbol{q}\|\)	0	7	1	1	4
Velocity		\(m/s\), \(rad/s\)	\(rad/s\)	\(m/s\)	\(rad/s\)
Position		\(m\), \(rad\)	\(rad\)	\(m\)	\(rad\)
Force		\(N\), \(Nm\)	\(Nm\)	\(N\)	\(Nm\)

The generalized coordinates/velocities of a joint are expressed in the joint frame and with respect to the parent body. Joint frame is the frame attached to every joint and fixed to the parent body. Parent body is the one closer to the root body among the two bodies connected via the joint. Note that the angular velocity of a floating base is also expressed in the parent frame (which is the world frame). Other libraries (e.g., RBLD) might have a different convention and a special care has to be taken in conversions.

URDF convention¶

RaiSim uses a modified URDF protocol to define an articulated system. URDF files following the original convention can be read in RaiSim. However, since RaiSim offers more functionalities, a RaiSim URDF might not be read by other libraries following the original URDF convention.

The modifications are as follows:

Capsule geom is available for both collision objects and visual objects (with the keyword “capsule”). The geom is defined by “height” and “radius” keyword. The height represents the distance between the two center points of the spheres.
A <joint>/<dynamics> tag can have three more attributes: rotor_inertia, spring_mount and stiffness.

Here is an example joint with the raisim tags

<joint name="link1Tolink2" type="spherical">
    <parent link="link1"/>
    <child link="link2"/>
    <origin xyz="0 0 -0.24"/>
    <axis xyz="0 1 0"/>
    <dynamics rotor_inertia="0.0001" spring_mount="0.70710678118 0 0.70710678118 0" stiffness="500.0" damping="3."/>
</joint>

Rotor_inertia in Raisim approximately simulates the rotor inertia of the motor (but missing the resulting gyroscopic effect, which is often neglegible).

It is added to the diagonal elements of the mass matrix. It is common way to include the inertial effect of the rotor. You can also override it in C++ using setRotorInertia(). Since RaiSim does not know the gear ratio, you have to multiply the rotor inertia by the square of the gear ratio yourself. In other words, the value is the reflected rotor inertia observed at the joint.

And two preprocessor features (that are also available in the raisim world configuration file) are available for the URDF template.

You can specify a variable in a form of “@@Robot_Height”. The value of this variable can be specified at the run timeusing ‘’std::unordered_map’’ and the corresponding factory method in ‘’raisim::World::.
You can specify an equation instead of a variable. For example, {@@Robot_Height*@@Robot_Width*2}.

The preprocessor example can be found in examples/src/server/trackedRobotAndTemplatedURDF.cpp and the corresponding URDF template in rsc/templatedTrackedRobot/trackedTemplate.urdf.

In RaiSim, each body of an articulated system has a set of collision bodies and visual objects. Collision bodies contain a collision object of one of the following shapes: mesh, sphere, box, cylinder, capsule. Visual objects just store specifications for visualization and the actual visualzation happens in a visualizer (e.g., raisimOgre) For details, check the URDF protocol.

Templated URDF¶

You can template an URDF and create different robots by providing different parameters in C++. An example can be found in here.

In the URDF template, variables should be marked with @@. Just like in a world configuration template, you can write math expressions inside {}. Only basic functions (i.e., sin, cos, log, exp) are available.

Template parameters should be provided at runtime in raisim::World::addArticulatedSystem. One of the overloading methods take const std::unordered_map<std::string, std::string>& params as input. The first one in the pair is the name and the second one is the parameter in a form of string.

Kinematics¶

Frames¶

A position and velocity of a specific point on a body of an articulated system can be obtained by attaching a frame. Frames are rigidly attached to a body of the system and has a constant position and orientation (w.r.t. parent frame). It is the most recommended way to get kinematics information of a point of an articulated system in RaiSim.

All joints have a frame attached and their names are the same as the joint name. To create a custom frame, a fixed frame can be defined at the point of the interest. A dummy link with zero inertia and zero mass must be added on one side of the fixed joint to complete the kinematic tree.

A frame can be locally stored as an index in the user code. For e.g.,

#include “raisim/World.hpp”

int main() {
  raisim::World world;
  auto anymal = world.addArticulatedSystem(PATH_TO_URDF);
  auto footFrameIndex = anymal->getFrameIdxByName("foot_joint"); // the URDF has a joint named "foot_joint"
  raisim::Vec<3> footPosition, footVelocity, footAngularVelocity;
  raisim::Mat<3,3> footOrientation;
  anymal->getFramePosition(footFrameIndex, footPosition);
  anymal->getFrameOrientation(footFrameIndex, footOrientation);
  anymal->getFrameVelocity(footFrameIndex, footVelocity);
  anymal->getFrameAngularVelocity(footFrameIndex, footAngularVelocity);
}

You can also store a Frame reference. For e.g., you can replace getFrameIdxByName by getFrameByName in the above example. In this way, you can access the internal variables and even modify them. Modifying the frames do not affect the joints. Frames are instantiated during initialization of the articulated system instance and affect neither kinematics nor dynamics of the system even if you change them.

Joint limits¶

Joint limits can be defined in an URDF file per joint as following

<limit effort="80" lower="-6.28" upper="6.28" velocity="15"/>

The lower and upper are joint position limits and the velocity is the joint velocity limit. The joint limits are implemented as if there is a hard stop at the limits. This means that there is a hard collision (with 0 restitution of coefficient) when the joint hits a limit.visualization

You modify the position joint limits in C++ using raisim::ArticulatedSystem::setJointLimits(). Currently, you cannot modify the velocity joint limits in code.

During simulation, you can get information on joint limit violations using raisim::ArticulatedSystem::getJointLimitViolations. Even though joint limits are collisions (and thus handled by a contact solver), they are not listed in raisim::Object::getContacts().

Jacobians¶

Jacobians of a point in RaiSim satisfy the following equation:

\[\begin{equation} \boldsymbol{J}\boldsymbol{u} = \boldsymbol{v} \end{equation}\]

where \(\boldsymbol{v}\) represents the linear velocity of the associated point. If a rotational Jacobian is used, the right-hand side changes to a rotational velocity expressed in the world frame.

To get the Jacobians associated with the linear velocity, the following methods are used

getSparseJacobian
getDenseJacobian – this method only fills non-zero values. The matrix should be initialized to a zero matrix of an appropriate size.

To get the rotational Jacobians, the following methods are used

getSparseRotationalJacobian
getDenseRotationalJacobian – this method only fills non-zero values. The matrix should be initialized to a zero matrix of an appropriate size.

The main Jacobian class in RaiSim is raisim::SparseJacobian. RaiSim uses only sparse Jacobians as it is more memory-friendly. Note that only the joints between the child body and the root body affect the motion of the point.

The class raisim::SparseJacobian has a member idx which stores the indicies of columns whose values are non-zero. The member v stores the Jacobian except the zero columns. In other words, ith column of v corresponds to idx[i] generalized velocity dimension.

Dynamics¶

All force and torque acting on the system can be represented as a single vector in the generalized velocity space. This representation is called generalized force \(\boldsymbol{\tau}\). Just like in a Cartesian coordiate (i.e., x, y, z axes), the power exerted by an articulated system is computed as a dot product of generalized force and generalized velocity (i.e., \(\boldsymbol{u}\cdot\boldsymbol{\tau}\)).

We can also combine the mass and inertia of the whole articulated system and represent them in a single matrix. This matrix is called mass matrix or inertia matrix and denoted by \(\boldsymbol{M}\). A mass matrix represents how much the articulated system resists change in generalized velocities. Naively speaking, a large mass matrix means that the articulated system experiences a low velocity change for a given generalized force.

The total kinetic energy of the system is computed as \(\frac{1}{2}\boldsymbol{u}^T\boldsymbol{M}\boldsymbol{u}\). This quantity can be obtained by getKineticEnergy().

The total potential energy due to the gravity is a sum of \(mgh\) for all bodies. This quantity can be obtained by getPotentialEnergy(). Note that the gravity has to be specified since only the world has the gravity vector.

The equation of motion of an articulated system is shown below:

\[\begin{equation} \boldsymbol{\tau} = \boldsymbol{M}(\boldsymbol{q})\dot{\boldsymbol{u}} + \boldsymbol{h}(\boldsymbol{q}, \boldsymbol{u}). \end{equation}\]

Here \(\boldsymbol{h}\) is called a non-linear term. There are three sources of force that contributes to the non-linear term: gravity, coriolis, and centrifugal force. It is rarely useful to compute the gravity contribution to the nonlinear term alone. However, if it is needed, the easiest way is to make the same robot in another world with zero velocity. If the generalized velocity is zero, the coriolis and centrifugal contributions are zero.

The following methods are used to obtain dynamic quantities

getMassMatrix()
getNonlinearities()
getInverseMassMatrix()

Inverse Dynamics¶

Raisim can compute Inverse Dynamics using the recursive newton euler algorithm. It is the only option for computing the force and torque acting at joints. Joint force/torque are sum of the constraint joint force/torque and actuation force/torque. For example, a revolute joint constrains motions in 5 degrees of freedom, which means that there are 5-dimensional constraint forces/torque and 1-dimensional joint actuation torque acting at a revolute joint.

In minimal coordinate simulation (such as Raisim), these constraint forces/torques are not computed in the simulation loop. These forces/torques can be computed after a simulation loop using the inverse dynamics pipeline.

To enable inverse dynamics, you should call raisim::ArticulatedSystem::setComputeInverseDynamics(true). This flag is set automatically if the robot has an IMU sensor. Note that the inverse dynamics pipeline will slow down the simulation by about 10%.

After a simulation loop, you can call raisim::ArticulatedSystem::getForceAtJointInWorldFrame() and raisim::ArticulatedSystem::getTorqueAtJointInWorldFrame() to get forces and torque acting at the specified joint.

Assuming that there are no joint position/velocity limit forces acting at the joint, you can compute the joint actuation as a dot product of the joint axis and the joint torque. An example can be found in examples/server/inverseDynamics.cpp.

PD Controller¶

When naively implemented, a PD controller can often make a robot unstable. However, this is often not so bad for robotics since this instability is also present in the real system (discrete-time control system).

For other applications like animation and graphics, it is often desirable to have a stable PD controller when a user wants to keep the time step small. Therefore, this PD controller exploits a more stable integration scheme and can have much smaller time step than a naive implementation.

This PD controller does not respect the actuation limits of the robot. It uses an implicit integration scheme and we do not even compute the actual torque that is applied to the joints.

To use this PD controller, you have to set the desirable control gains first

Eigen::VectorXd pGain(robot->getDOF()), dGain(robot->getDOF());
pGain<< ...; // set your proportional gain values here
dGain<< ...; // set your differential gain values here
robot->setPdGains(pGain, dGain);

Note that the dimension of the pGain vector is the same as that of the generalized velocity NOT that of the coordinate.

Finally, the target position and the velocity can set as below

Eigen::VectorXd pTarget(robot->getGeneralizedCoordinateDim()), vTarget(robot->getDOF());
pTarget<< ...; // set your position target
vTarget<< ...; // set your velocity target
robot->setPdTarget(pTarget, vTarget);

Here, the dimension of the pTarget vector is the same as that of the generalized coordinate NOT that of the velocity. This is confusing and might seem inconsistent. However, this is a valid convention. The only reason that the two dimensions differ is quaternions. The quaternion target is represented by a quaternion whereas the virtual spring stiffness between the two orientations can be represented by a 3D vector, which is composed of motions in each angular velocity components.

A feedforward force term can be added by setGeneralizedForce() if desired. This term is set to zero by default. Note that this value is stored in the class instance and does not change unless the user specifies it so. If this feedforward force should be applied for a single time step, it should be set to zero in the subsequent control loop (after integrate() call of the world).

The theory of the implemented PD controller can be found in chapter 1.2 of this article. This document is only for advanced users and it is not necessary to use RaiSim.

Integration Steps¶

Integration of an articulated systems is performed in two stages: integrate1 and integrate2

The following steps are performed in integrate1

If the time step is changed, update the damping of the mass matrix (which reflects effective inertial increase due to springs, dampers and PD gains)
Update positions of the collision bodies
Detect collisions (called by the world instance)
The world assigns contacts on each object and computes the contact normal
Compute the mass matrix, nonlinear term and inverse inertia matrix
Compute (Sparse) Jacobians of contacts

After this step, all kinematic/dynamic proerpties are computed at this stage. Users can access them if they are necessary for the controller. Next, integrate2 computes the rest of the simulation.

Compute contact Properties
Compute PD controller (if used), add it to the feedforward force and bound it by the limits
Compute generalized forces due to springs and external forces/torques
Contact solver (called by the world instance)
Integrate the velocity
Integrate the position (in a semi-implicit way)

Get and Modify Robot Description in code¶

RaiSim allows users modify most of the robot parameters freely in code. This allows users to create randomized robot model, which might be useful for AI applications (i.e., dynamic randomization). Note that a random model might be kinematically and dynamically unrealistic. For example, joints can be locked by collision bodies. In such cases, simulation cannot be performed reliably and it is advised to carefully check randomly generated robot models.

Here is a list of modifiable kinematic/dynamic parameters.

Joint Position (relative to the parent joint) Expressed in the Parent Frame

getJointPos_P method returns (a non-const reference to) a std::vector of position vectors from the parent joint to the child joint expressed in the respective parent joint frames. This should be changed with care since it can result in unrealistic collision geometry. This method does not change the position of the end-effector with respect to its parent as the position of the last link is defined by the collision body position, not by the joint position. The elements are ordered by the joint indicies.

Joint Axis in the Parent Frame

getJointAxis_P method returns (a non-const reference to) a std::vector of joint axes expressed in the respective parent joint frame. This method should also be changed with care. The elements are ordered by the joint indicies.

Mass of the Links

getMass method returns (a non-const reference to) a std::vector of link masses. IMPORTANT! You must call :code:`updateMassInfo` after changing mass values. The elements are ordered by the body indicies (which is the same as the joint indicies in RaiSim).

Center of Mass Position

getBodyCOM_B method returns (a non-const reference to) a std::vector of the COM of the bodies. The elements are ordered by the body indices.

Link Inertia

getInertia method returns (a non-const reference to) a std::vector of link inertia. The elements are ordered by the body indicies.

Collision Bodies

getCollisionBodies method returns (a non-const reference to) a std::vector of the collision bodies. This vector contains all collision bodies associated with the articulated system.

getCollisionBody method returns a specific collision body instead. All collision bodies are named “LINK_NAME” + “/INDEX”. For example, the 2nd collision body of a link named “FOOT” is named “FOOT/1” (1 because the index starts from 0).

The collision bodies is a class that contains position/orientation offset from the parent joint frame, name, parent body index, and ODE collision pointer (dGeomID, retrieved using getCollisionObject). The collision geom can be modified using ODE methods (ODE manual). Users can also modify the material of the collision body. This material affects the contact dynamics.

Apply External Forces/torques¶

The following two methods are used to apply external force and torque respectively

setExternalForce
setExternalTorque

You will find above methods in the API section on this page.

Collision¶

Apart from the collision mask and collision group set in the world, users can also disable a collision between a certain pair of the links with ignoreCollisionBetween.

Types of Indicies¶

ArticulatedSystem class contains multiple types of indicies. To query a specific quantity, you have to provide an index of the right type. Here are the types of indicies in Articulated Systems

Body/Joint Index: All fixed bodies are combined to a single movable body. Each movable body has a unique body index. Because there is a movable joint associated with a movable body, there is a 1-to-1 mapping between the joints and the bodies and they share the same index. For a fixed-base system, the first body rigidly fixed to the world is body-0. For a floating-base system, the floating base is body-0.
Generalized Velocity (DOF) Index: All joints are mapped to a specific set of generalized velocity indicies.
Generalized Coordinate Index:
Frame Index:

Conversions Between Indicies¶

A body index to a generalized velocity index: ArticulatedSystem::getMappingFromBodyIndexToGeneralizedVelocityIndex()
A body index to a generalized coordinate index: ArticulatedSystem::getMappingFromBodyIndexToGeneralizedCoordinateIndex()

API¶

class ArticulatedSystem : public raisim::Object ¶

Public Functions

inline const raisim::VecDyn &getGeneralizedCoordinate() const¶

Returns: generalized coordinate of the system

inline const raisim::VecDyn &getGeneralizedVelocity() const¶

Returns: generalized velocity of the system

inline const raisim::VecDyn &getGeneralizedAcceleration() const¶

Returns: generalized acceleration of the system. The generalized acceleration is computed in the integration step. So this function does not work properly if you have not integrated the world.

void getBaseOrientation(raisim::Vec<4> &quaternion) const¶

Parameters: quaternion – [out] orientation of base

inline void getBaseOrientation(raisim::Mat<3, 3> &rotataionMatrix) const¶

Parameters: rotataionMatrix – [out] orientation of base

inline const raisim::Mat<3, 3> &getBaseOrientation() const¶

Returns: orientation of base

inline void getBasePosition(raisim::Vec<3> &position) const¶

Parameters: position – [out] position of base

inline raisim::Vec<3> getBasePosition() const¶

Returns: position of base

void updateKinematics()¶: unnecessary to call this function if you are simulating your system. integrate1 calls this function Call this function if you want to get kinematic properties but you don’t want to integrate.

inline void setGeneralizedCoordinate(const Eigen::VectorXd &jointState)¶

set gc of each joint in order

Parameters: jointState – [in] generalized coordinate

inline void setGeneralizedCoordinate(const raisim::VecDyn &jointState)¶

set gc of each joint in order

Parameters: jointState – [in] generalized coordinate

inline void setGeneralizedVelocity(const Eigen::VectorXd &jointVel)¶

set the generalized velocity

Parameters: jointVel – [in] the generalized velocity

inline void setGeneralizedVelocity(const raisim::VecDyn &jointVel)¶

set the generalized velocity

Parameters: jointVel – [in] the generalized velocity

void setGeneralizedCoordinate(std::initializer_list<double> jointState)¶

set the generalized coordinsate of each joint in order.

Parameters: jointState – [in] the generalized coordinate

void setGeneralizedVelocity(std::initializer_list<double> jointVel)¶

set the generalized velocity of each joint in order

Parameters: jointVel – [in] the generalized velocity

void setGeneralizedForce(std::initializer_list<double> tau)¶

This is feedforward generalized force. In the PD control mode, this differs from the actual generalizedForce the dimension should be the same as dof.

Parameters: tau – [in] the generalized force. If the built-in PD controller is active, this force is added to the generalized force from the PD controller

inline void setGeneralizedForce(const raisim::VecDyn &tau)¶

This is feedforward generalized force. In the PD control mode, this differs from the actual generalizedForce the dimension should be the same as dof.

Parameters: tau – [in] the generalized force. If the built-in PD controller is active, this force is added to the generalized force from the PD controller

inline void setGeneralizedForce(const Eigen::VectorXd &tau)¶

This is feedforward generalized force. In the PD control mode, this differs from the actual generalizedForce the dimension should be the same as dof.

Parameters: tau – [in] the generalized force. If the built-in PD controller is active, this force is added to the generalized force from the PD controller

inline void getState(Eigen::VectorXd &genco, Eigen::VectorXd &genvel) const¶

get both the generalized coordinate and the generalized velocity

Parameters

genco – [out] the generalized coordinate
genvel – [out] the generalized velocity

inline void getState(VecDyn &genco, VecDyn &genvel) const¶

get both the generalized coordinate and the generalized velocity

Parameters

genco – [out] the generalized coordinate
genvel – [out] the generalized velocity

inline void setState(const Eigen::VectorXd &genco, const Eigen::VectorXd &genvel)¶

set both the generalized coordinate and the generalized velocity. This updates the kinematics and removes previously computed contact points

Parameters

genco – [in] the generalized coordinate
genvel – [in] the generalized velocity

inline VecDyn getGeneralizedForce() const¶

Generalized user-set gen force (using setGeneralizedForce()). This method a small error when the built-in PD controller is used. The PD controller is implicit (using a continuous, linear model) so we cannot get the true gen force. But if you set the time step small enough, the difference is negligible.

Returns: the generalized force

inline const VecDyn &getFeedForwardGeneralizedForce() const¶

get the feedfoward generalized force (which is set by the user)

Returns: the feedforward generalized force

inline const MatDyn &getMassMatrix()¶

get the mass matrix

Returns: the mass matrix. Check Object/ArticulatedSystem section in the manual

inline const VecDyn &getNonlinearities(const Vec<3> &gravity)¶

get the coriolis and the gravitational term

Parameters: gravity – [in] gravitational acceleration. You should get this value from the world.getGravity();
Returns: the coriolis and the gravitational term. Check Object/ArticulatedSystem section in the manual

inline const MatDyn &getInverseMassMatrix()¶

get the inverse mass matrix. Note that this is actually damped inverse. It contains the effect of damping and the spring effects due to the implicit integration. YOU MUST CALL getMassMatrix FIRST BEFORE CALLING THIS METHOD.

Returns: the inverse mass matrix. Check Object/ArticulatedSystem section in the manual

inline const std::vector<raisim::Vec<3>> &getCompositeCOM() const¶

get the center of mass of a composite body containing body i and all its children. if you want the COM of the whole robot, just take the first element This only works if you have called getMassMatrix() with the current state

Returns: the center of mass of the composite body

inline Vec<3> getCOM() const¶

get the center of mass of the whole system

Returns: the center of mass of the system

inline const std::vector<raisim::Mat<3, 3>> &getCompositeInertia() const¶

get the current composite inertia of a composite body containing body i and all its children

Returns: the inertia of the composite system

inline const std::vector<double> &getCompositeMass() const¶

get the current composite mass of a composite body containing body i and all its children

Returns: get the composite mass

inline Vec<3> getLinearMomentum() const¶

linear momentum of the whole system

Returns: momentum

inline const VecDyn &getGeneralizedMomentum() const¶

returns the generalized momentum which is M * u It is already computed in “integrate1()” so you don’t have to compute again.

Returns: the generalized momentum

double getEnergy(const Vec<3> &gravity)¶

Parameters: gravity – [in] gravitational acceleration
Returns: the sum of potential/kinetic energy given the gravitational acceleration

double getKineticEnergy()¶

Returns: the kinetic energy.

double getPotentialEnergy(const Vec<3> &gravity) const¶

Parameters: gravity – [in] gravitational acceleration
Returns: the potential energy (relative to zero height) given the gravity vector

void getAngularMomentum(const Vec<3> &referencePoint, Vec<3> &angularMomentum) const¶

Parameters

referencePoint – [in] the reference point about which the angular momentum is computed
angularMomentum – [in] angular momentum about the reference point

void printOutBodyNamesInOrder() const¶: bodies here means moving bodies. Fixed bodies are optimized out

void printOutMovableJointNamesInOrder() const¶: print out movable joint names in order

void printOutFrameNamesInOrder() const¶: frames are attached to every joint coordinate

inline const std::vector<std::string> &getMovableJointNames() const¶

getMovableJointNames. Note! the order doesn’t correspond to dof since there are joints with multiple dof’s

Returns: movable joint names in the joint order.

inline size_t getGeneralizedVelocityIndex(const std::string &name) const¶

get generalized velocity index of a joint.

Returns: the joint index.

virtual void getPosition(size_t bodyIdx, const Vec<3> &point_B, Vec<3> &point_W) const final¶

Parameters

bodyIdx – [in] The body which contains the point, can be retrieved by getBodyIdx()
point_B – [in] The position of the point in the body frame
point_W – [out] The position of the point in the world frame

Returns

position in the world frame of a point defined in a joint frame

inline CoordinateFrame &getFrameByName(const std::string &nm)¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details

Parameters: nm – [in] name of the frame
Returns: the coordinate frame of the given name

inline CoordinateFrame &getFrameByLinkName(const std::string &name)¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details

Parameters: name – [in] name of the urdf link that is a child of the joint
Returns: the coordinate frame of the given link name

inline size_t getFrameIdxByLinkName(const std::string &name) const¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details

Parameters: name – [in] name of the urdf link that is a child of the joint
Returns: the coordinate frame index of the given link name

inline CoordinateFrame &getFrameByIdx(size_t idx)¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details

Parameters: idx – [in] index of the frame
Returns: the coordinate frame of the given index

size_t getFrameIdxByName(const std::string &nm) const¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details The frame can be retrieved as as->getFrames[index]. This way is more efficient than above methods that use the frame name

Parameters: nm – [in] name of the frame
Returns: the index of the coordinate frame of the given index. Returns size_t(-1) if it doesn’t exist

inline std::vector<CoordinateFrame> &getFrames()¶

Refer to Object/ArticulatedSystem/Kinematics/Frame in the manual for details The frame can be retrieved as as->getFrames[index]. This way is more efficient than above methods that use the frame name

Returns: a vector of the coordinate frames

void getFramePosition(size_t frameId, Vec<3> &point_W) const¶

Parameters

frameId – [in] the frame id which can be obtained by getFrameIdxByName()
point_W – [out] the position of the frame expressed in the world frame

void getPositionInFrame(size_t frameId, const Vec<3> &localPos, Vec<3> &point_W) const¶

Parameters

frameId – [in] the frame id which can be obtained by getFrameIdxByName()
localPos – [in] local position in the specified frame
point_W – [out] the position expressed in the world frame

void getFrameOrientation(size_t frameId, Mat<3, 3> &orientation_W) const¶

Parameters

frameId – [in] the frame id which can be obtained by getFrameIdxByName()
orientation_W – [out] the position of the frame relative to the world frame

void getFrameVelocity(size_t frameId, Vec<3> &vel_W) const¶

Parameters

frameId – [in] the frame id which can be obtained by getFrameIdxByName()
vel_W – [out] the linear velocity of the frame expressed in the world frame

void getFrameAngularVelocity(size_t frameId, Vec<3> &angVel_W) const¶

Parameters

frameId – [in] the frame id which can be obtained by getFrameIdxByName()
angVel_W – [out] the angular velocity of the frame expressed in the world frame

inline void getFramePosition(const std::string &frameName, Vec<3> &point_W) const¶

Parameters

frameName – [in] the frame name (defined in the urdf)
point_W – [out] the position of the frame expressed in the world frame

inline void getFrameOrientation(const std::string &frameName, Mat<3, 3> &orientation_W) const¶

Parameters

frameName – [in] the frame name (defined in the urdf)
orientation_W – [out] the orientation of the frame relative to the world frame

inline void getFrameVelocity(const std::string &frameName, Vec<3> &vel_W) const¶

Parameters

frameName – [in] the frame name (defined in the urdf)
vel_W – [out] the linear velocity of the frame expressed in the world frame

inline void getFrameAngularVelocity(const std::string &frameName, Vec<3> &angVel_W) const¶

Parameters

frameName – [in] the frame name (defined in the urdf)
angVel_W – [out] the angular velocity of the frame relative to the world frame

void getFramePosition(const CoordinateFrame &frame, Vec<3> &point_W) const¶

Parameters

frame – [in] custom frame defined by the user
point_W – [out] the position of the frame relative to the world frame

void getFrameOrientation(const CoordinateFrame &frame, Mat<3, 3> &orientation_W) const¶

Parameters

frame – [in] custom frame defined by the user
orientation_W – [out] the orientation of the frame relative to the world frame

void getFrameVelocity(const CoordinateFrame &frame, Vec<3> &vel_W) const¶

Parameters

frame – [in] custom frame defined by the user
vel_W – [out] the linear velocity of the frame expressed to the world frame

void getFrameAngularVelocity(const CoordinateFrame &frame, Vec<3> &angVel_W) const¶

Parameters

frame – [in] custom frame defined by the user
angVel_W – [out] the angular velocity of the frame expressed to the world frame

inline void getFrameAcceleration(const std::string &frameName, Vec<3> &acc_W) const¶

YOU NEED TO ENABLE INVERSEDYNAMICS COMPUTATION TO USE THIS METHOD This is time derivative of (body velocity expressed in the world frame). If you premultiply this by the transpose of the rotation matrix of the frame, it is the same as what your accelerometer sensor will measure if you place it at the frame (but an IMU has gravity bias so they will be off by the gravitational acceleration). This is not the same as {(time derivative of body velocity expressed in the body frame) expressed in the world frame}

Parameters

frameName – [in] name of the frame
acc_W – [out] the linear acceleration of the frame expressed in the world frame

inline void getFrameAcceleration(const CoordinateFrame &frame, Vec<3> &acc_W) const¶

YOU NEED TO ENABLE INVERSEDYNAMICS COMPUTATION TO USE THIS METHOD This is time derivative of (body velocity expressed in the world frame). If you premultiply this by the transpose of the rotation matrix of the frame, it is the same as what your accelerometer sensor will measure if you place it at the frame. (but an IMU has gravity bias so they will be off by the gravitational acceleration). This is not the same as {(time derivative of body velocity expressed in the body frame) expressed in the world frame}

Parameters

frame – [in] custom frame defined by the user
acc_W – [out] the linear acceleration of the frame expressed in the world frame

inline virtual void getPosition(size_t bodyIdx, Vec<3> &pos_w) const final¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
pos_w – [out] the position of the joint (after its own joint transformation)

void getPositionInBodyCoordinate(size_t bodyIdx, const Vec<3> &pos_W, Vec<3> &pos_B)¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
pos_W – [in] the position in the world coordinate. This position does not have to be physically on the body.
pos_B – [out] the position in the body frame

inline virtual void getOrientation(size_t bodyIdx, Mat<3, 3> &rot) const final¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
rot – [out] the orientation of the joint (after its own joint transformation)

inline virtual void getVelocity(size_t bodyIdx, Vec<3> &vel_w) const final¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
vel_w – [out] the linear velocity of the joint (after its own joint transformation)

inline void getAngularVelocity(size_t bodyIdx, Vec<3> &angVel_w) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
angVel_w – [out] the angular velocity of the joint (after its own joint transformation)

void getSparseJacobian(size_t bodyIdx, const Vec<3> &point_W, SparseJacobian &jaco) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
point_W – [in] the point expressed in the world frame. If you want to use a point expressed in the body frame, use getDenseFrameJacobian()
jaco – [out] the positional Jacobian. v = J * u. v is the linear velocity expressed in the world frame and u is the generalized velocity

void getSparseJacobian(size_t bodyIdx, Frame frame, const Vec<3> &point, SparseJacobian &jaco) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
frame – [in] the frame in which the position of the point is expressed in
point – [in] the point expressed in the world frame. If you want to use a point expressed in the body frame, use getDenseFrameJacobian()
jaco – [out] the positional Jacobian. v = J * u. v is the linear velocity expressed in the world frame and u is the generalized velocity

void getSparseRotationalJacobian(size_t bodyIdx, SparseJacobian &jaco) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
jaco – [out] the rotational Jacobian. omega = J * u. omgea is the angular velocity expressed in the world frame and u is the generalized velocity

void getTimeDerivativeOfSparseJacobian(size_t bodyIdx, Frame frame, const Vec<3> &point, SparseJacobian &jaco) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
frame – [in] the frame in which the position of the point is expressed
point – [in] the position of the point of interest
jaco – [out] the time derivative of the positional Jacobian. a = dJ * u + J * du. a is the linear acceleration expressed in the world frame, u is the generalized velocity and d denotes the time derivative

void getTimeDerivativeOfSparseRotationalJacobian(size_t bodyIdx, SparseJacobian &jaco) const¶

Parameters

bodyIdx – [in] the body index. Note that body index and the joint index are the same because every body has one parent joint. It can be retrieved by getBodyIdx()
jaco – [out] the rotational Jacobian. alpha = dJ * u + J * du. alpha is the angular acceleration expressed in the world frame, u is the generalized velocity and d denotes the time derivative

inline void getDenseJacobian(size_t bodyIdx, const Vec<3> &point_W, Eigen::MatrixXd &jaco) const¶